0.什么场景下会用到bloom filter

  1. 缓存穿透
  2. 爬虫重复 URL 检测， 避免爬虫过程形成环
  3. 假设有 10 亿条手机号，然后判断某条手机号是否在列表内
  4. 唯一昵称判断

这些场景可以用什么方式解决

  1. hashmap, hashset
  2. MySQL：正常情况下，如果数据量不大，我们可以考虑使用 mysql 存储。将所有数据存储到数据库，然后每次去库里查询判断是否存在。但是如果数据量太大，超过千万，mysql 查询效率是很低的，特别消耗性能。
  3. bitmap
  4. bloom filter

1.bloom filter 是什么？

布隆过滤器是一种概率性数据结构，它提供了一种空间效率极高的方法来测试一个元素是否属于一个集合。

其基本原理是使用多个不同的哈希函数对元素进行哈希，然后将得到的哈希值对应到位数组上。一个元素被加入到集合中，那么所有哈希函数计算出的位置都会被置为1。检查元素是否存在于集合中时，使用这些哈希函数计算哈希值，并检查对应的位是否都是1。如果都是1，那么元素可能存在于集合中；如果任何一个位不是1，那么元素肯定不在集合中。

其主要特点是：

  • 高空间效率：相比于传统的集合数据结构，布隆过滤器使用极少的空间来处理大量数据。
  • 误报率/假阳：布隆过滤器有一定的误报概率，这意味着它可能会错误地认为某个不在集合中的元素存在于集合中。
  • 零漏报率：不会遗漏集合中真正存在的元素
  • 不可删除：标准的布隆过滤器不支持从集合中删除元素，尽管存在变种（如计数布隆过滤器）支持这一操作。
  • 多哈希函数：布隆过滤器通过多个哈希函数来减少误报率，每个元素被多个哈希函数映射到位数组的多个位置。

1.1 为什么空间效率高

bloom filter 采用 位数组（bit array）作为核心的数据结构。

位数组是一个非常紧凑的数据结构，它可以有效地表示大量的布尔值（true或false），每个值只占用一个位（bit），而不是使用更传统的数据类型会占用更多的空间。

比如在爬虫场景中，假设有1亿个URL，每个URL算4字节, 如果用hashmap 实现，一个URL所占空间至少4bytes;如果用位数组实现，每个URL 所占的空间仅1bit，空间效率提升了32倍（存储空间不考虑误判率的前提下）。不可谓不高效。

1.2 为什么会有误报率/假阳

既然用到了哈希函数，肯定会遇到哈希冲突。所以一个元素对应 的n 个位置， 可能因为其他元素的哈希冲突 而导致判断时发现等于1， 从而产生假阳现象。

1.3 误报如何解决

假阳问题无法被避免，只能尽可能减少。 减少的途径是选择合适的哈希函数以及指定合适的空间大小

1.4 为什么需要多个哈希函数

布隆过滤器的设计使用多个哈希函数来解决单个哈希函数可能带来的局限性，提高其效率和准确性。具体来说，使用多个哈希函数的原因包括：

  • 降低误报率

    通过使用多个哈希函数独立地映射每个元素到位数组中的多个位置，并在所有这些位置上标记为1，可以显著降低不同元素映射到相同位置（即产生冲突）的概率，从而降低误报率

  • 均匀分布

    多个哈希函数可以将元素更均匀地分布在位数组上，减少了集中冲突的可能性。如果只使用一个哈希函数，即使其分布性质良好，也难以保证对于所有可能的输入集合都能保持良好的均匀性。多个哈希函数的组合，如果设计得当，可以相互补偿，实现更为均匀的分布。

1.5 为什么数据不可删除

在布隆过滤器中，元素的存在是通过多个位的“1”状态来表示的，而将这些位重置为“0”可能会错误地影响其他元素的存在检测。

如果需要支持删除，可以考虑使用 变体Bloom Filter， 如cuckoo filter

2. bitmap 和 bloom filter 的区别

Bitmap（位图）和布隆过滤器都是使用空间效率高的数据结构，它们通过利用位操作来实现存储和查询，但它们的设计目的和应用场景有所不同。

2.1 Bitmap（位图）

位图是一种数据结构，用于高效地存储和查询状态信息。在位图中，每个元素的存在或状态是由单独的位来表示的，即使用1位二进制数（0或1）来表示每个元素是否存在或某种特定状态。

主要特点和用途：

  • 简单直接：适用于需要追踪大量元素（如整数）存在与否的场景。
  • 空间效率：对于大规模数据集，位图使用的空间远小于传统的数据结构（如数组或列表）。
  • 随机访问：可以非常快速地检查任何一个元素的存在与否或状态。

  • 固定大小：位图的大小在创建时由最大元素值决定，因此其空间效率依赖于数据的分布。

  • BitMap 的实现
    java BitSet
    redis setbit、getbit

2.2 区别

  • 用途：位图主要用于精确表示一个大型数据集中元素的存在与否或状态信息，而布隆过滤器用于以极小的空间成本判断元素是否可能存在于集合中。
  • 错误率：位图提供了100%准确的结果（假设足够的空间来表示所有元素），而布隆过滤器允许一定的误报率。
  • 操作：位图支持添加、查询和删除（通过位反转）操作，而标准布隆过滤器不支持删除操作。
  • 空间效率与数据规模：布隆过滤器在表示大型集合成员资格时通常比位图更加空间效率，尤其是当元素范围非常大但实际元素数量相对较少时。

总之，位图和布隆过滤器各有优势和应用场景，选择哪种数据结构取决于具体需求，包括对空间效率、准确率和操作类型的要求。

3. 单机版本Guava Cache 源码解析

3.1 create

1
2
3
4
5
6
7
public static <T> BloomFilter<T> create(Funnel<T> funnel, int expectedInsertions /* n */,  
    double falsePositiveProbability) {  
    int numBits = optimalNumOfBits(expectedInsertions, falsePositiveProbability);  
    int numHashFunctions = optimalNumOfHashFunctions(expectedInsertions, numBits);  
    return new BloomFilter<T>(new BitArray(numBits), numHashFunctions, funnel,  
BloomFilterStrategies.MURMUR128_MITZ_32);  
}

3.1.1 参数解释

  • funnel：Funnel类型的参数，用于将任意类型的数据转化成布隆过滤器内部使用的一种形式。Funnel定义了如何把对象转换成二进制流，然后布隆过滤器使用这个二进制流来计算元素的哈希值。

  • expectedInsertions：这个参数指定了预期要插入布隆过滤器的元素数量。这个数值是为了优化布隆过滤器内部数据结构的大小。

  • falsePositiveProbability（false positive probability）：误判率。这是指一个不存在集合中的元素被判断为存在的概率。值得注意的是，随着实际插入数量的增加，实际的误判率可能会上升。

3.1.2 optimalNumOfBits

1
2
3
static int optimalNumOfBits(int expectedInsertions, double falsePositiveProbability) {  
	return (int) (-n * Math.log(p) / LN2_SQUARED);  
}

optimalNumOfBits通过计算,可以得到一个在满足特定假阳性率（falsePositiveProbability）要求下，对于给定数量的元素预期插入量（expectedInsertions），所需的最少位数。这使得布隆过滤器能够在保证误判率的前提下，使用最少的空间。这种计算对于设计高效且空间节约的布隆过滤器至关重要

3.1.3 计算逻辑

optimalNumOfBits函数的计算基于以下公式，这个公式可以从布隆过滤器的理论误判率公式推导而来：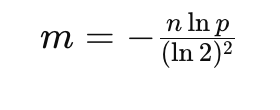

  • m 是位数组的长度（即函数的返回值）。
  • n 是expectedInsertions，即预期的插入数量。
  • p 是falsePositiveProbability，即期望的假阳性概率。
  • ln⁡2 表示自然对数。
    这个公式利用了布隆过滤器的误判率特性，通过指定的假阳性率和预期插入数量来计算出一个最优的位数组长度。这个长度能够在满足误判率要求的同时，尽可能地减小布隆过滤器所需的空间。

3.1.4 实现注意

实际实现时，可能还需要对计算结果进行取整处理，并确保结果是一个正整数。此外，实现可能还会考虑到性能和存储效率的平衡，比如通过限制位数组的长度为2的幂等。

3.1.5 optimalNumOfHashFunctions

1
2
3
static int optimalNumOfHashFunctions(int n, int m) {  
	return Math.max(1, (int) Math.round(m / n * LN2));  
}

optimalNumOfHashFunctions(expectedInsertions, numBits)这个函数用于计算给定条件下布隆过滤器的最优哈希函数数量。这个计算基于预期要插入的元素数量（expectedInsertions）和布隆过滤器内部位数组的大小（numBits）。目的是为了平衡空间使用和误判率，确保布隆过滤器在给定条件下工作得最有效率。

计算逻辑

布隆过滤器的效率和误判率与使用的哈希函数数量有很大关系。太少的哈希函数会增加碰撞的概率，导致误判率升高；而太多的哈希函数又会导致位数组快速填满，同样增加误判率，同时还会增加计算的开销。

最优哈希函数数量的计算公式是：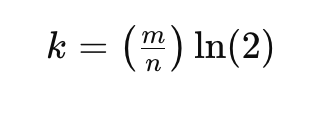

这个公式基于以下原理：给定一个固定大小的位数组，存在一个最优的哈希函数数量，可以最小化给定元素数量条件下的误判率。这个最优数量直接关联于位数组的大小和要处理的元素数量。

其中：

  • k 是最优的哈希函数数量，
  • m 是位数组的大小（numBits），
  • n 是预期插入的元素数量（expectedInsertions），
  • ln⁡(2) 是自然对数2的值，大约等于0.693。

3.1.6 new BitArray(numBits)

Guava cache bloom filter 在实现位数组是采用创建long[] + 位移操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
static class BitArray {  
final long[] data;  
  
BitArray(int bits) {  
    this(new long[IntMath.divide(bits, 64, RoundingMode.CEILING)]);  
}  
  
// Used by serialization  
BitArray(long[] data) {  
    checkArgument(data.length > 0, "data length is zero!");  
    this.data = data;  
}  
  
void set(int index) {  
    data[index >> 6] |= (1L << index);  
}  
  
boolean get(int index) {  
    return (data[index >> 6] & (1L << index)) != 0;  
}  
  
/** Number of bits */  
int size() {  
    return data.length * Long.SIZE;  
}  
}

3.2 put

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
MURMUR128_MITZ_32() {  
@Override public <T> void put(T object, Funnel<? super T> funnel,  
int numHashFunctions, BitArray bits) {  
// TODO(user): when the murmur's shortcuts are implemented, update this code  
long hash64 = Hashing.murmur3_128().newHasher().putObject(object, funnel).hash().asLong();  
int hash1 = (int) hash64;  
int hash2 = (int) (hash64 >>> 32);  
for (int i = 1; i <= numHashFunctions; i++) {  
int nextHash = hash1 + i * hash2;  
if (nextHash < 0) {  
nextHash = ~nextHash;  
}  
// up to here, the code is identical with the next method  
bits.set(nextHash % bits.size());  
}  
}

首先，这行代码使用MurmurHash3算法生成一个128位的哈希值，然后将其转换成一个long类型的数值hash64。

  • funnel是一个函数式接口，用于将对象转换为字节流，以便哈希函数可以处理。
  • hash64实际上包含两个32位的哈希值，它们可以从hash64的高32位和低32位分别提取。从hash64中提取两个32位的哈希值hash1和hash2。hash1是低32位，hash2是高32位。
    • 接下来，代码遍历从1到numHashFunctions（布隆过滤器要求的哈希函数数量），每次循环计算一个新的哈希值nextHash。这个新的哈希值是通过hash1 + i * hash2计算得到的，其中i是当前的迭代次数。
  • 如果nextHash为负数，通过位取反操作（~nextHash）将其转换为正数，以保证能够正确地映射到位数组的索引上。
  • 最后，使用nextHash % bits.size()计算得到的索引值在位数组（BitArray）中对应的位置上设置位。bits.size()返回位数组的大小，这确保了计算得到的索引值不会超出位数组的范围。

3.2.1 哈希函数

Guava cache 采用了非加密的单向散列函数Murmur3.
MurmurHash 由Austin Appleby设计，因其高性能和良好的分布特性而广泛应用。MurmurHash有多个版本，如MurmurHash2、MurmurHash3等。

根据最开始对bloom filter 的定义，它需要多个哈希函数对数据进行哈希映射， 但Guava Cache bloom filter 实现中其实没有使用多个不同的哈希函数，而是采用了一种叫做“双哈希技术”的方法。

“双哈希技术”的基本思想是利用两个哈希函数h1(x)和h2(x)生成任意数量的哈希值，对于第i个哈希位置，使用h1(x) + i*h2(x)的方式来生成。这种方法只需要两次哈希操作，就可以模拟出多个哈希函数的效果，且生成的哈希序列具有很好的均匀分布性，既保证了布隆过滤器的效率，又避免了寻找多个好的哈希函数的复杂性，是一种在实际应用中非常实用的解决方案。

效率和复杂性具体指

  1. 性能和效率：使用单个哈希函数后通过算法变换生成多个哈希值，可以大大减少计算的复杂度和时间。多个独立的哈希函数意味着每个元素都需要被多次独立哈希，这会增加计算成本和时间。通过使用单个哈希函数并通过数学方法派生出多个伪随机的哈希值，可以在保持布隆过滤器错误率不变的前提下，显著提高效率。
  2. 简化实现：多个不同的哈希函数难以选取，而且还需保证它们相互之间的独立性和分布的均匀性，这在实践中是非常挑战性的。

3.3 mightContains

和put 处理过程保持一致

3.4 guava cache 误报率-位数组长度固定

在使用Guava的布隆过滤器时，预先估计将要插入的数据量非常重要。布隆过滤器在创建时会根据这个预估的数据量和指定的误判率来决定位数组的大小和使用的哈希函数数量。这些参数共同决定了布隆过滤器的性能和准确性。

如果实际插入的元素数量超过了最初的预估，过滤器的实际误判率会高于预期的误判率。这是因为当位数组变得过于饱和时，不同元素的哈希值更有可能映射到已经被设置为1的位上，从而增加了误判的几率。

Guava的文档明确指出了这一点，强调在创建布隆过滤器时应该准确预估元素数量，并考虑到这一点在其API设计中。BloomFilter.create()方法允许开发者在创建过滤器时指定预期插入的元素数量和可接受的误判率。

https://guava.dev/releases/20.0/api/docs/com/google/common/hash/BloomFilter.html

为了保证布隆过滤器的效果，应该根据实际使用场景仔细估算元素数量。如果预计数据量存在不确定性，建议预估一个上限，或者在实际元素数量超过预估时重新创建一个新的布隆过滤器。这当然会带来额外的成本，因此在设计初期做出准确估计非常关键。

总结来说，正确估计将要处理的数据量对于使用Guava布隆过滤器来说是非常重要的。如果实际数据量超过了预估，将会导致高于预期的误判率，可能影响到应用的准确性和可靠性。

4. 分布式 Redis bloom filter

1
BF.RESERVE {key} {error_rate} {capacity} [EXPANSION expansion] [NONSCALING]

4.1 参数解释

4.1.1 EXPANSION expansion

BF.RESERVE命令是RedisBloom模块中用来创建一个新的布隆过滤器的命令。这个命令允许用户预先为布隆过滤器指定参数，以便在插入元素之前就确定其大小和其他重要的行为特性。以下是BF.RESERVE命令各个参数的含义：

  • {key}：这是将要创建的布隆过滤器的名称或键值。在Redis中，每个数据结构都通过一个唯一的键来标识和访问。

  • {error_rate}：预期的误报率。这是一个0到1之间的浮点数，表示允许的误判概率的上限。误报率越低，布隆过滤器所需的空间就越大。

  • {capacity}：布隆过滤器预期要存储的元素的数量。这个数值用于在保持误报率不变的情况下，预先计算布隆过滤器所需的最小大小。

  • [EXPANSION expansion]（可选）：这个可选参数用于指定当布隆过滤器的容量不足以容纳更多元素时，自动扩展的行为。expansion是一个大于1的整数，表示每次扩展增加的比例或容量。如果未指定，布隆过滤器可能会使用默认的扩展策略。

  • [NONSCALING]（可选）：这个可选标志用来指示创建的布隆过滤器不应自动扩展。这意味着一旦达到其容量上限，就不会尝试扩大过滤器以容纳更多的元素。这通常用于那些对空间使用有严格限制的应用场景。

  • 作用：这个参数用于设置布隆过滤器在达到容量限制并需要扩展时，新创建的布隆过滤器层的大小。expansion的值决定了新层的容量是前一层容量的多少倍。这是一种自动扩展布隆过滤器容量的机制，以适应不断增长的元素数量，同时控制误报率。

  • 场景：适用于那些元素数量不确定或可能会超出初始设定容量的场合。通过适当设置expansion参数，可以在维持误报率的同时动态增加布隆过滤器的容量。
  • 举例：如果设置[EXPANSION 2]，那么每次扩展时，新的布隆过滤器层的容量将是前一层的两倍。

4.1.2 NONSCALING

  • 作用：指定创建的布隆过滤器为非扩展型（Non-scaling）。即，一旦创建，布隆过滤器的容量固定，不会根据元素的增加而自动增加新的层。这意味着所有元素都将被添加到这个固定大小的布隆过滤器中，不管其容量是否已满。
  • 场景：适用于元素数量预先已知且不会超出初始设定容量的场合。这种方式可以避免因为扩展而可能带来的额外内存使用，但要求用户必须更准确地预估所需的容量和误报率。

注意：当使用[NONSCALING]参数时，[EXPANSION expansion]参数将无效，因为非扩展型的布隆过滤器不会进行任何扩展操作。

4.2 可拓展特性是如何实现

redis 可扩展布隆过滤(Scalable Bloom Filters)可以理解成是由多个位数组/子过滤器（布隆过滤器实例）链接在一起形成的链表(SBChain)。

每个子过滤器都有其自己的容量和误报率设置。当前的子过滤器达到容量限制时，就会动态地添加一个新的子过滤器。

这种方法的关键优势是，它可以在不断增加元素的情况下，动态地扩展总容量，同时控制整体误报率。

然而，这种动态扩展的能力也意味着查询操作可能需要遍历链表中的多个布隆过滤器实例，这可能会对性能产生一定影响。

redis bloom filter 的整体上的基本逻辑，比如位数组的大小、选择的哈希函数、哈希函数的数量、多个哈希函数的模拟与Guava cache bloom filter基本保持一致， 接下来只重点分析其可拓展性是如何实现的

4.2.1 bloom 结构体

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bloom.h

struct bloom {  
uint32_t hashes;  
uint8_t force64;  
uint8_t n2;  
uint64_t entries;  
  
double error;  
double bpe;  
  
unsigned char *bf;  
uint64_t bytes;  
uint64_t bits;  
};

这个struct bloom定义了一个布隆过滤器的基本数据结构，用于在RedisBloom模块中表示一个布隆过滤器实例。下面是对各个成员变量的详细解释：

  • uint32_t hashes;：这表示布隆过滤器使用的哈希函数的数量。在布隆过滤器中，元素的存在是通过多个哈希函数映射到位数组的不同位置来表示的。因此，哈希函数的数量直接影响布隆过滤器的误判率和效率。
  • uint8_t force64;：这是一个标志位，用于指示是否强制使用64位哈希函数。在某些情况下，为了保证在不同平台上的一致性和性能，可能需要强制使用64位哈希函数。
  • uint8_t n2;：这个成员可能用于表示与位数组大小相关的一个参数，具体含义取决于实现细节。在一些布隆过滤器的实现中，这个参数可能与位数组大小为2的幂次方有关。
  • uint64_t entries;：这表示预期存储在布隆过滤器中的元素数量。这个数值对于计算位数组的大小和哈希函数数量非常重要。
  • double error;：这是预期的误判率（false positive rate），是设计布隆过滤器时的一个关键参数。误判率越低，所需的位数组大小和哈希函数数量就越多。
  • double bpe;：这表示每个元素平均占用的位数（Bits Per Entry）。这个值是根据预期的误判率和元素数量计算得出的，用于确定位数组的大小。
  • unsigned char *bf;：这是一个指向位数组的指针。位数组是布隆过滤器的核心，用于存储元素的哈希值映射。unsigned char类型被用来表示位数组，每个字节包含8位。
  • uint64_t bytes;：这表示位数组占用的字节数。由于位数组是以字节为单位进行分配的，因此这个数值表示整个位数组的大小。
  • uint64_t bits;：这表示位数组中的位数。这个数值是根据entries、error和bpe计算得出的，决定了布隆过滤器可以有效存储的元素数量和误判率。

4.2.2 SBLink结构体

1
2
3
4
5
6
sb.h
/** Single link inside a scalable bloom filter */  
typedef struct SBLink {  
struct bloom inner; //< Inner structure  
size_t size; // < Number of items in the link  
} SBLink;

SBLink代表了可扩展布隆过滤器中的单个链接，即单个布隆过滤器实例。

  • struct bloom inner;：这是一个嵌套的结构体，表示单个布隆过滤器的内部结构。这个inner结构体可能包含了实现布隆过滤器所需的所有数据，如位数组、哈希函数数量等。
  • size_t size;：表示当前链接（即单个布隆过滤器实例）中的元素数量。这是为了快速访问单个过滤器内元素的数量，而无需遍历整个位数组。

4.2.3 SBChain结构体

1
2
3
4
5
6
7
8
9
sb.h  
/** A chain of one or more bloom filters */  
typedef struct SBChain {  
SBLink *filters; //< Current filter  
size_t size; //< Total number of items in all filters  
size_t nfilters; //< Number of links in chain  
unsigned options; //< Options passed directly to bloom_init  
unsigned growth;  
} SBChain;

SBChain代表了一系列（一个或多个）SBLink结构体的链表，构成了一个可扩展的布隆过滤器。

  • SBLink *filters;：这是一个指向SBLink数组的指针，表示当前所有的过滤器链。每个SBLink代表链中的一个布隆过滤器实例。
  • size_t size;：表示所有过滤器中元素的总数量。这个数字是所有单个SBLink中size成员的总和。
  • size_t nfilters;：表示链中SBLink实例的数量，即当前有多少个布隆过滤器被链接在一起。
  • unsigned options;：这是传递给每个布隆过滤器初始化函数bloom_init的选项。这些选项可能控制如布隆过滤器的误报率、是否自动扩展等行为。
  • unsigned growth;：这个成员变量控制链的增长行为。它可能指定当当前的布隆过滤器填满时，如何增加新的SBLink实例，例如，增加的大小或比例等。

4.3 可扩展bloom filter的工作流程

  1. 初始化：当创建一个新的可扩展布隆过滤器时，会指定初始容量、误报率等参数。基于这些参数，创建第一个子过滤器。
  2. 添加元素：向布隆过滤器添加元素时，会从当前子过滤器开始尝试添加。如果当前子过滤器已满（即达到了其容量限制），则创建一个新的子过滤器，并在新的子过滤器中添加元素。每个新添加的子过滤器都可以根据配置的规则调整大小和误报率，以适应不断增加的元素。
  3. 检查元素：检查一个元素是否存在时，需要查询所有的子过滤器。如果任何子过滤器表示元素可能存在（即对应的位都为1），则认为元素可能存在于布隆过滤器中。虽然可扩展布隆过滤器可以动态增加容量，但查询操作的成本随之增加，因为可能需要检查多个布隆过滤器实例。
  4. 参数调整：随着子过滤器的增加，每个新的子过滤器通常会有更大的容量。这是通过调整如比特数、哈希函数数量等参数来实现的。这种方法旨在平衡误报率和内存使用，即使在不断添加元素的情况下也能维持相对稳定的误报率。

5. 可删除 bloom filter

5.1 哪些场景使用布隆过滤器时需要删除

以上， guava 和 redis 的bloom filter 都没有实现删除功能，不能删除的原因已经解释过，元素的存在是通过多个位的“1”状态来表示的，而将这些位重置为“0”可能会错误地影响其他元素的存在检测。

但是在某些场景还是需要删除，比如，
查看一张优惠券是否已被使用？创建一个包含所有存在但还未被使用优惠券的filter。每次校验时

  • 如果否，则优惠券不存在。
  • 如果是，则优惠券有效。检查主数据库。如果有效，则使用后从 Cuckoo 过滤器中删除。

5.2 实现删除布隆过滤器的思路

5.2.1 计数型布隆过滤器（Counting Bloom Filter）

这是最直接的方法之一，它通过为每个位使用一个计数器而不是简单的布尔标记来实现。当插入一个元素时，它经过多个哈希函数映射到多个计数器上，并将这些计数器的值增加。相应地，删除一个元素时，这些计数器的值会被减少。如果任何计数器的值达到零，则表示没有任何元素映射到这个位上。这种方法的缺点是需要更多的空间来存储计数器。

5.2.2 双布隆过滤器

这种方法涉及到使用两个独立的布隆过滤器：一个用于添加操作，另一个用于删除操作。当添加一个元素时，它被添加到第一个布隆过滤器中；当删除一个元素时，该元素被添加到第二个布隆过滤器中。检查元素是否存在时，如果它在第一个布隆过滤器中并且不在第二个布隆过滤器中，则认为该元素存在。这种方法的问题是误报率会增加，因为删除过滤器中的元素也可能错误地阻止对实际存在于集合中的元素的正确判断。

5.2.3 d-left 计数哈希

d-left计数哈希是一种高效的数据结构，它将元素映射到固定数量的桶中，并在每个桶内维护一个计数器。这种方法可以实现快速的插入、查询和删除操作，并且相比于计数型布隆过滤器，它可以更有效地利用空间。不过，实现起来比较复杂，且当桶填满时性能会下降。

5.2.4 布谷鸟过滤器（Cuckoo Filter）

布谷鸟过滤器是另一种支持删除操作的布隆过滤器变种，它基于布谷鸟哈希和部分键存储。每个元素通过哈希函数映射到一个或多个位置，并存储其“指纹”。插入、查询和删除操作都基于这些指纹。布谷鸟过滤器相比计数型布隆过滤器在空间效率上有所提高，且支持删除操作，但在极端情况下可能需要重建过滤器。

总体上可以看出可删除bloom filter 的实现都是需要额外的空间去存储额外的信息， 那么其实现方式的好坏的评判标准就是 额外空间的大小、性能 以及对误报率的影响。

以下是一张表格，总结了几种支持删除操作的布隆过滤器变体的优点和缺点：

过滤器类型 优点 缺点
计数型布隆过滤器 - 直接支持删除操作
- 实现相对简单		 - 更多空间需求
- 计数器溢出问题
双布隆过滤器 - 实现简单
- 通过额外布隆过滤器跟踪删除操作		 - 增加空间需求
- 误判率增加
布谷鸟过滤器 - 高效的插入、删除和查询
- 空间效率高		 - 实现复杂
- 负载因子高时性能可能下降
d-left计数哈希过滤器 - 高空间效率
- 性能优于传统计数型布隆过滤器		 - 实现复杂，需要精心设计
  • 如果应用对空间效率要求不是特别高，且需要频繁进行删除操作，计数型布隆过滤器是一个简单有效的选择。
  • 对于需要最小化误报率而且对空间有一定要求的应用，布谷鸟过滤器提供了一个较好的平衡点。
  • 在需要极致空间效率且能够接受实现复杂度的高性能应用场景中，d-left 计数哈希过滤器可能是最佳选择。

关于空间的使用，有如下比对效果

redis 实现了cuckoo 变体bloom filter， 下面来讲一下 cuckoo filter 的原理

6. Cuckoo Filter

Cuckoo Filter 论文

the basic unit of the cuckoo hash tables used for our cuckoo filters is called an entry. Each entry stores one fingerprint. The hash table consists of an array of buckets, where a bucket can have multiple entries.

在Cuckoo Filter 中，最基本的存储单元是entry, 每个单元存储一个 fingerprint。cuckoo hashing 哈希表由一组桶（buckets）组成，每个桶可以包含多个条目（entries）。

Cuckoo Filter的关键特性

  1. 双哈希函数：对于任何一个给定的键，Cuckoo Hashing使用两个独立的哈希函数 h1 和 h2 来计算两个候选桶的位置。这两个位置是键可能被存储的地方。
  2. 指纹存储：与传统的哈希表不同，Cuckoo Hashing不存储完整的键，而是存储键的指纹。这允许在不牺牲太多空间效率的情况下进行高效的查找和删除操作。
  3. 动态插入：当插入一个新键时，如果候选桶中没有足够的空间，Cuckoo Hashing会通过一系列置换操作来为新键腾出空间。这涉及到将现有的指纹移动到它们的替代位置，从而为新键腾出空间。已占用位置的元素会被移动到其它哈希函数确定的位置，可能导致一个连锁的重新放置过程。这个算法的名字来源于布谷鸟，因为布谷鸟会将自己的蛋放入其他鸟类的巢中，迫使其他鸟类的蛋被移位或丢弃。
  4. 查找操作：给定一个键，Cuckoo Hashing通过检查两个候选桶中的指纹来确定键是否存在于表中。如果任一桶中存在匹配的指纹，则认为键存在于表中。
  5. 删除操作：删除操作相对简单，Cuckoo Hashing检查两个候选桶，如果找到匹配的指纹，则移除该指纹。这种删除方法不会影响其他键的存储位置。
  6. 高空间效率：Cuckoo Hashing通过存储指纹而不是完整的键来优化空间使用，同时保持较高的表占用率，从而实现高空间效率。

6.1 fingerprint

“fingerprint”是存储在Cuckoo Filter中的数据。，一个哈希函数处理数据后得到的哈希串。

6.2 Partial-Key Cuckoo Hashing

A cuckoo filter is a compact variant of a cuckoo hash table that stores only fingerprints-a bit string derived from the item using a hash function。

在cuckoo filter 中，哈希表中存储的数据发生了变化，由原始数据变成了fingerprint。
注意这里的（basic/standard） cuckoo hash tables指的是存储原始数据的做法。

partial-key cuckoo hashing 是一种仅使用指纹，而不需要原始数据就可以在置换操作中来确定元素存储位置的哈希技术。由于仅存储fingerprint 比存储原始数据所占内存空间小，所以 Partial-Key Cuckoo Hashing为优化Cuckoo Filter的空间效率和操作性能而设计。

如上代码所示，Partial-Key Cuckoo Hashing使用两个哈希函数 h1 和 h2 来计算两个候选桶位置。第一个哈希函数 h1 直接作用于元素的指纹，而第二个哈希函数 h2 则是 h1 与指纹的哈希值的异或（XOR）结果。
这种XOR的处理结果 可以根据其中任意一个已知的候选桶位置（i）计算出另外一个候选桶位置（j）
j = i XOR fingerprint

6.3 Insert

cuckoo 哈希的插入过程：

  1. 计算元素的指纹。
  2. 确定两个候选桶位置 i1 和 i2。
  3. 如果 i1 或 i2 有空闲条目，则将指纹插入到该条目中。
  4. 如果两个桶都满，则选择一个桶，随机选择一个条目并将其指纹与新元素的指纹交换。
  5. Partial-Key Cuckoo Hashing ，更新候选桶位置 i 为 i XOR 指纹的哈希值。
  6. 如果找到空闲条目，则插入指纹；否则继续置换过程，直到找到空闲条目或达到最大置换次数。

6.4 Lookup

6.5 Delete

为什么cuckoo filter 可以删除元素但是又不影响其他元素的判断， 其实就是每个entry 只存储了一个元素的信息，删除后自然不会影响其他元素的判断。

6.6 空间优化

Cuckoo Filter进行空间优化（SPACE OPTIMIZATIONS）的方法主要涉及对哈希表参数的选择和配置，以及对桶（buckets）的编码策略。以下是论文中提到的一些关键的空间优化策略：

  1. 选择合适的桶大小（Bucket Size）：
    • 桶大小（b）对Cuckoo Filter的空间效率有显著影响。较大的桶可以提高哈希表的占用率（α），但同时也需要更长的指纹来维持相同的误报率。
    • 论文中通过实验确定了对于不同的目标误报率（ϵ），最优的桶大小是不同的。例如，当误报率大于0.002时，每个桶有2个条目可能比4个条目更有效；而当误报率降低到0.00001至0.002时，每个桶有4个条目可以最小化空间使用。
  2. 半排序桶编码（Semi-Sorting Buckets）：
    • 对于每个桶中的指纹进行排序，然后使用一个预先计算好的表来编码这些排序后的指纹序列。由于桶内指纹的顺序不影响查询结果，这种方法可以通过索引来节省空间。
    • 例如，如果每个桶有4个指纹，每个指纹是4比特长，那么未压缩的桶将占用16比特。通过排序和编码，可以使用一个12比特的索引来代替原来的16比特桶，因为可以预先计算出所有可能的桶值（例如，3876种），并将每个桶表示为一个索引，从而节省1比特每个指纹。
  3. 平衡桶的负载（Balancing Bucket Loads）：
    • 通过合理配置哈希函数和桶大小，可以减少哈希表中的冲突和空桶，从而提高空间利用率。
    • 论文中提到，通过适当的配置，Cuckoo Filter可以以高概率达到95%的表空间占用率。
  4. 指纹长度的优化：
    • 指纹长度（f）与桶大小和目标误报率有关。通过调整指纹长度，可以在保持目标误报率的同时，优化空间使用。
    • 论文中的分析表明，对于实际应用中的集合大小，较短的指纹（例如6比特或更长）通常足以确保哈希表的高利用率。

通过这些空间优化策略，Cuckoo Filter能够在保持高效动态操作的同时，实现紧凑的数据存储。这些优化使得Cuckoo Filter在很多实际应用中比传统的Bloom Filter和Counting Bloom Filter更加空间高效

6.7 Redis cuckoo filter

redis 实现了 cuckoo filter ，基本实现逻辑和论文中表现一致，有兴趣大家可以自己去看一下

7. 自己如何实现一个布隆过滤器

基于以上对3种bloom filter的分析，可以总结出自己实现bloom filter时需要考虑的因素
本项目代码可点击这里查看

7.1 位数组的实现

首先参考BitSet。
BitSet类是Java标准库中提供的一个用于处理位数组的类，基本可以认为是bitmap 在Java 的中的实现，其原理是是long[] 数组+ 位操作。
在自己实现布隆过滤器时，可以直接使用BitSet ， 也可以像guava cache 一样，自己用long[] + 位操作自己封装一个bitarray，而不是直接使用的BitSet。

7.2 位数组的大小

在简单的自己实现的版本中，可以直接指定bitarray 大小。

但在实际线上生产环境中可用的bloom filter 实现，一般都是根据预期插入的数据量 和 可接受的误报率两个数字通过 一个数学公式算出的，而不是直接用预期插入的数据量。

同时我们在线上生产环境使用布隆过滤器时，根据业务特性和流量去估算预期插入的数据量 和衡量 可接受的误报率 也是非常重要的步骤。 如果估算数据量比实际值大很多，就会浪费内存空间。如果估算数据量比实际值小很多，那么误报率很可能就无法控制在可接受的范围内。

  1. guava cache bloom filter 位数组大小一旦确定时无法修改的，所以实际数据量如果过大，那么误报率肯定会上升
  2. redis bloom filter 位数组大小可以scale, 但是判断元素是否存在的这个步骤性能会受到影响

7.3 用哪个哈希函数

这个哈希函数在密码学中叫做单向散列函数。单向散列函数有两类
加密与非加密散列，其主要区别如下。

7.3.1 加密散列函数

设计用于加密应用，强调安全性。它们需要具备一定的性质，如抗碰撞（两个不同的输入不应该产生同一个输出）、隐藏性（无法从输出推断任何信息关于输入）和抗篡改（对输入的微小变化会在输出中产生不
可预测的、大的变化）。

  • SHA家族（SHA-1、SHA-256、SHA-512等）：安全哈希算法（Secure Hash Algorithm）家族，广泛用于加密、数据完整性校验和数字签名等安全相关的应用。
  • MD5：消息摘要算法5（Message Digest Algorithm 5），尽管因为安全性问题不再推荐用于加密安全领域，但在一些非安全性要求的场合仍然可以见到其身影。
  • RIPEMD：一系列的加密哈希函数，包括RIPEMD-160、RIPEMD-256和RIPEMD-320，其中RIPEMD-160设计用于替代MD5和SHA-1。
    -

    7.3.2 非加密散列函数

    设计重点是高效率和均匀分布的输出，以支持快速数据检索、数据分布平衡等，而不是安全性。在某些情况下，允许存在碰撞，但碰撞的概率要尽可能低。

常见的非加密单向散列函数：

  1. MurmurHash：由Austin Appleby设计，因其高性能和良好的分布特性而广泛应用。MurmurHash有多个版本，如MurmurHash2、MurmurHash3等。
  2. CityHash：由Google开发，专为哈希字符串数据设计，适用于构建哈希表等数据结构。后续Google又推出了FarmHash，作为CityHash的改进版，提供更好的性能和更广的适用范围。
  3. xxHash：是一种非常快的哈希算法，提供了极高的数据处理速度，同时保持了良好的散列分布特性，适用于需要快速散列大量数据的场景。
  4. Jenkins哈希函数（如一致性哈希）：Bob Jenkins所设计的一系列哈希函数，包括lookup3、SpookyHash等，它们广泛用于软件开发中，特别是在需要快速且分布均匀的哈希算法的场合。
  5. FNV（Fowler-Noll-Vo）：是一系列设计简单、性能良好的哈希函数，特别适合于散列单个文本字符串。FNV-1和FNV-1a是两个最著名的变种。

在以上分析原理分析中，guava cache和Redis 都是用了MurmurHash
如果我们自己也想要用MurmurHash，目前Java并没有提供实现，可以引入guava cache 包使用MurmurHash。

7.4 用多少个哈希函数

前面说过用多个哈希函数可以减少误报率，那么到底要用多少个哈希函数呢， 这也是可以通过 预期插入的数据量+ 可接受的误报率 通过固定的数学公式计算得出。
同时多个哈希结果可以通过像Guava cache一样，用双哈希技术模拟得到。

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。